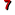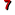|
Final Version - MS L75.350-357
|
MEMOIR 1
ON THE CLASSIFICATION OF
THE THEORETIC SCIENCES OF RESEARCH
This will be a natural classification, not of possible sciences,
but of sciences as they exist today; not of sciences in the sense of
"systematized knowledge," but of branches of endeavor to ascertain
truth. I shall not undertake to prove that there is no other natural
classification of the sciences than that which I give; and this, being
merely an introductory memoir, cannot have the same convincing
character as the others. Every unitary classification has a leading
idea or purpose, and is a natural classification in so far as that
same purpose is determinative in the production of the objects
classified. The purpose of this classification is nearly the same as
that of Comte, namely, so to arrange a catalogue of the sciences as to
exhibit the most important of |351| the relations of logical dependence
among them. In fact, my classification is simply an attempt to
improve upon that of Comte; first, by looking less at what has been
the course of scientific history, and more at what it would have been
if the theoretically best methods had been pursued; second, by
supplying the shocking omissions which Comte's rage against nonsense
led him to commit; and third, by carrying down the subdivision as far
as my knowledge enables me to do. It was necessary for me to determine what I should call one
science. For this purpose I have united under one science studies
such as the same man, in the present state of science, might very well
pursue. I have been guided in determining this by noting how
scientists associate themselves into societies, and what contributions
are commonly admitted into one journal, being on my guard against the
survival of traditions from bygone states of science. A study to which men devote their lives, but not, in the present
stage of development of science, so numerously as to justify exclusive
societies and journals for it, I call a variety of science. That
which forms the subject of the narrowest societies and journals, so
that any student of any part of it ought to be pretty thoroughly
informed about every part, I call a species of science. That branch
of which the student of any part is well qualified to take up any
other part, except that he may not be sufficiently acquainted with the
facts in detail, I call a genus of science. If the only new training
necessary to pass from one part to another is a mere matter of skill,
the general conceptions remaining the same, I call the department a
family of science. If different sorts of conceptions are dealt with
in the different families of a depart|353|ment, but the general type of
inquiry is the same, I call it an order of science. If the types of
inquiry of the different orders of a department are different, yet
these orders are connected together so that students feel that they
are studying the same great subject, I call the department a class of
science. If there are different classes, so that different students
seem to live in different worlds, but yet there is one general
animating motive, I call the department a branch of science. Of
course, there will be sub-branches, sub-classes, etc., down to
sub-varieties; and even sometimes sub-sub-divisions. To illustrate, I
call pure science and applied science different branches, and call
mathematics and the special sciences different classes; I say that
general physics, biology, and geology belong to different orders of
science. Astronomy and geognosy are different families. Thermotics
and electrics are different families. Optics and electrics |354| are now
different genera. Entomology and ichthyology are different species of
one genus. The study of Kant and the study of Spinoza are different
varieties of one species.
Of course, the execution of this useful but ambitious design can,
in the first instance, notwithstanding all the labor on my part that
seemed economically recommended, be but a sketch. It will have fully
attained all I hope for if it is respectable enough to merit serious
picking to pieces in its smaller and in its larger divisions. Indeed,
I may say of all these memoirs that what I most desire is that their
errors should be exposed, so long as they lead to further scientific
study of the subjects to which they relate. The relation of this
present memoir to those which follow it in the series is that it
gives, from a general survey of science, an idea of the place of logic
among the sciences. I will here set down the larger divisions of the
scheme as well as I remember it (not having the notes in my
possession). But it will be the discussion which will form the chief
value of the memoir, not the |355| scheme itself. Nearly a hundred schemes
given hitherto will be criticized.
A. Theoretical Science
I. Science of Research
i. Mathematics
ii. Philosophy, or Cenoscopy
1. Categorics [= phenomenology or phaneroscopy]
2. Normative Science
a. Esthetics
b. Ethics
c. Logic [= semiotic]
[philosophical grammar]
[critical logic]
[philosophical rhetoric]
3. Metaphysics
iii. Idioscopy, or Special Science
1. Psychognosy
a. Nomological or General Psychology
b. Classificatory
 . Linguistics . Linguistics
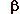 . Critics . Critics
 . Ethnology |356| . Ethnology |356|
c. Descriptive
 . Biography . Biography
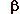 . History . History
 . Archeology . Archeology
2. Physiognosy
a. Nomological or General Physics
 . Dynamics . Dynamics
1. Of particles
2. Of aggregations
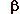 . Elaterics and Thermotics . Elaterics and Thermotics
 . Optics and Electrics . Optics and Electrics
b. Classificatory
 . Crystallography . Crystallography
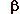 . Chemistry . Chemistry
 . Biology . Biology
c. Descriptive
 . Astronomy . Astronomy
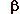 . Geognosy |357| . Geognosy |357|
II. Science of Review, or Synthetic Philosophy
(Humboldt's Cosmos; Comte's Philosophie Positive)
B. Practical Science, or the Arts
| EDITORIAL NOTE: Bracketed material in the above scheme is
editorially supplied as a clarification. Josiah (Lee) Auspitz has objected, though, that the simple identification of logic in the broad sense with semeiotic (also spelled "semiotic" by Peirce) is not correct. His reasons for this are not clear to me and I believe the currently prevailing opinion is in agreement with my own view that they are supposed to be identical; but Lee Auspitz is a careful and talented scholar and his dissent is worth taking special note of. Perhaps he can be persuaded to write up a critical note to that effect which we can add to the present presentation by including it through a hypertext link. This invitation applies to anyone else as well who wants to take exception to any of my editorial interpretation here or simply wants to add something to it by way of commentary for further elucidation: write it up as a criticism or commentary and we will put a hypertext link-button for that note in the text itself, thus making it an addendum to the present account. |
|
From Draft E - MS L75.206-207
|
This [classification] would be restricted to sciences as they
actually exist, with some little provision of what is sure to be
brought about soon. It would consider sciences, not as "systematized
knowledge," but as organizations of research, as they live today. My
classification of the applied sciences, or arts, not having been very
successful, I should probably not attempt to go into that subject.
Moreover, such studies as Humboldt's Cosmos, and Comte's
Philosophie Positive, although they are really studies of science,
would not fall within the scope of my classification, which would thus
be limited to the theoretical sciences. My classification is quite
minute; but its leading divisions are: mathematics; philosophy or, as
Bentham calls it, cenoscopic (i.e. based on universal experience); and
idioscopic, or special science. The last falls into two parts,
psychognosy (embracing psychology, linguistics, ethnology, history,
etc.) and physiognosy |207| (embracing physics, chemistry, biology,
astronomy, geognosy). I divide philosophy into three parts, the
categories, normative science (esthetics, ethics, and logic,) and
metaphysics. Geometry and the science of time form a connecting link
between metaphysics and idioscopy.
In constructing my classification, I have carefully studied the
reasons alleged for nearly a hundred other systems; so that the
critical part of this memoir would be extremely laborious. Yet as my
purpose is not to advance anything for which I cannot produce
convincing proof, such criticism must be carefully and respectfully
performed throughout all the memoirs.



|
Final Version - MS L75.357
|
MEMOIR 2
ON THE SIMPLEST MATHEMATICS
This is that mathematics which distinguishes only two different
values, and is of great importance for logic. 
|
From Draft E - MS L75.207
|
This is the system which has a scale of values of only two
degrees. Since these may be identified (in an application of this
pure mathematical system) as the true and the false, this system calls
for somewhat elaborate study as a propaedeutic to logic.



|
Final Version - MS L75.357
|
MEMOIR 3
ANALYSIS OF THE CONCEPTIONS OF MATHEMATICS
Such are number, multitude, limit, infinity, infinitesimals,
continuity, dimension, imaginaries, multiple algebra, measurement,
etc. My former contributions, though very fragmentary, have attracted
attention in Europe, although in respect to priority justice has not
been done them. I bring the whole together into one system, defend
the method of infinitesimals conclusively, and give many new truths
established by a new and striking method.
|
From Draft E - MS L75.208-209
|
My work in this direction is already somewhat known, although
very imperfectly. One of the learned academies of Europe has crowned
a demonstration that my definition of a finite multitude agrees with
Dedekind's definition of an infinite multitude. It appears to me that
the one is hardly more than a verbal modification of the other. I am
usually represented as having put forth my definition as a substitute
for Dedekind's. In point of fact, mine was published six years before
his; and my paper contains in very brief and crabbed form all the
essentials of his beautiful exposition (still more perfect as modified
by Schröder). Many animadversions have been made by eminent men upon
my remark, in the Century Dictionary, that the method of
infinitesimals is more consonant with then (in 1883) recent studies of
mathematical logic. In this memoir, I should show precisely how the
calculus may be, to the advantage of simplicity, based upon the
doctrine of infinitesimals. Many futile attempts have been made to
define continuity. In the sense in |209| the calculus, no difficulty
remains. But the whole of topical geometry remains in an exceedingly
backward state and destitute of any method of proof simply because
true continuity has not been mathematically defined. By a careful
analysis of the conception of a collection, of which no mathematical
definition has been yet published, I have succeeded in giving a
demonstration of an important proposition which Cantor had missed,
from which the required definition of a continuum results; and a
foundation is afforded for topical geometry, which branch of geometry
really embraces the whole of geometry. I have made several other
advances in defining the conceptions of mathematics which illuminate
the subject.



|
Final Version - MS L75.357
|
MEMOIR 4
ANALYSIS OF THE METHODS OF MATHEMATICAL DEMONSTRATION
I shall be glad to place early in the series so unquestionable an
illustration of the great value of minute analysis as this memoir will
afford. The subjects of corollarial and theorematic reasoning, of the
method of abstraction, of substantive possibility, |358| and of the method
of topical geometry, of which I have hitherto published mere hints,
will here be fully elaborated.
[This memoir] will examine the nature of mathematical reasoning.
Logic can pass no judgment upon such reasoning, because it is evident,
and as such, beyond all criticism. But logic is interested in
studying how mathematical reasoning proceeds. Mathematical reasoning
will be analyzed and important properties of it brought out which
mathematicians themselves are not aware of.
|
From Draft E - MS L75.209-210
|
I have hitherto only published some slight hints of my
discoveries in regard to the logical processes used in mathematics. I
find that two different kinds of reasoning are used, which I |210|
distinguish as the corollarial and the theorematic. This is a matter
of extreme importance for the theory of cognition. It remains
unpublished. I also find that the most effective kind of theorematic
demonstration always involves the long despised operation of
abstraction, which has been a common topic of ridicule. This is the
operation by which we transform the proposition that "Opium puts
people to sleep" into the proposition that "Opium has a soporific
virtue". Like every other logical transformation, it can be applied
in a futile manner. But I show that, without it, the mathematician
would be shut off from operations upon lines, surfaces, differentials,
functions, operations—and even from the consideration of cardinal
numbers. I go on to define precisely what it is that this operation
effects. I endeavor in this paper to enumerate, classify, and define
the precise mode of effectiveness of every method employed in
mathematics.
|
From Draft C - MS L75.90-102
|
No science of logic is needed for mathematics beyond that which
mathematics can itself supply, unless possibly it be in regard to
mathematical heuretic. But the examination of the methods of
mathematical demonstration shed |91| extraordinary light upon logic, such
as I, for my part, never dreamed of in advance, although I ought to
have guessed that there must be unexpected treasures hidden in this
quite unexplored ground. That the logic of mathematics belonged to
the logic of relatives, and to the logic of triadic, not of dyadic
relations, was indeed obvious in advance; but beyond that I had no
idea of its nature. The first things I found out were that all
mathematical reasoning is diagrammatic and that all necessary
reasoning is mathematical reasoning, no matter how simple it may be.
By diagrammatic reasoning, I mean reasoning which constructs a diagram
according to a precept expressed in general terms, performs
experiments upon this diagram, notes their results, assures itself
that similar experiments performed upon any diagram constructed
according to the same precept would have |92| the same results, and expresses
this in general terms. This was a discovery of no little importance,
showing, as it does, that all knowledge without exception comes from
observation.
At this point, I intend to insert a mention of my theory of
grades of reality. The general notion is old, but in modern times it
has been forgotten. I undertake to prove its truth, resting on the
principle that a theory which is adapted to the prediction of
observational facts, and which does not lead to disappointment, is
ipso facto true. This principle is proved in No. 1. Then my proof of
grades of reality is inductive, and consists in often turning aside in
the course of this series of memoirs to show how this theory is
adapted to the expression of facts. This might be mistaken for
repetitiousness; but in fact it is logically defensible, and it also
has the advantage of leading the reader, step by step, to the
compre|93|hension of an idea which he would not be able to grasp at once,
and to the appreciation of an argument which he could not digest at
one time. I will not here undertake to explain what the theory is in
detail. Suffice it to say that since reality consists in this, that a
real thing has whatever characters it has in its being and its having
them does not consist in its being represented to have them, not even
in its representing itself to have them, not even if the character
consists in the thing's representing itself to represent itself;
since, I say, that is the nature of reality, as all schools of
philosophy now admit, there is no reason in the nature of reality why
it should not have gradations of several kinds; and in point of fact,
we find convincing evidences of such gradations. It is easy to see
that according to this definition the square root of minus 1 possesses
a certain grade of |94| reality, since all its characters except only that
of being the square root of minus one are what they are whether you or
I think so or not. So when Charles Dickens was half-through one of
his novels, he could no longer make his characters do anything that
some whim of a reader might suggest without feeling that it was false;
and in point of fact the reader sometimes feels that the concluding
parts of this or that novel of Dickens is false. Even here, then,
there is an extremely low grade of reality. Everybody would admit
that the word might be applied in such cases by an apt metaphor; but I
undertake to show that there is a certain degree of sober truth in it,
and that it is important for logic to recognize that the reality of
the Great Pyramid, or of the Atlantic Ocean, or of the Sun itself, is
nothing but a higher grade of the same thing.
But to say that the reasoning of mathematics is |95| diagrammatic is
not to penetrate in the least degree into the logical peculiarities of
its procedure, because all necessary reasoning is diagrammatic.
My first real discovery about mathematical procedure was that
there are two kinds of necessary reasoning, which I call the
corollarial and the theorematic, because the corollaries affixed to
the propositions of Euclid are usually arguments of one kind, while
the more important theorems are of the other. The peculiarity of
theorematic reasoning is that it considers something not implied at
all in the conceptions so far gained, which neither the definition of
the object of research nor anything yet known about could of
themselves suggest, although they give room for it. Euclid, for
example, will add lines to |96| his diagram which are not at all required
or suggested by any previous proposition, and which the conclusion
that he reaches by this means says nothing about. I show that no
considerable advance can be made in thought of any kind without
theorematic reasoning. When we come to consider the heuretic part of
mathematical procedure, the question how such suggestions are obtained
will be the central point of the discussion.
Passing over smaller discoveries, the principal result of my
closer studies of it has been the very great part which an operation
plays in it which throughout modern times has been taken for nothing
better than a proper butt of ridicule. It is the operation of
abstraction, in the proper sense of the term, which, for example,
converts the |97| proposition "Opium puts people to sleep" into "Opium has
a dormitive virtue". This turns out to be so essential to the greater
strides of mathematical demonstration that it is proper to divide all
theorematic reasoning into the non-abstractional and the
abstractional. I am able to prove that the most practically important
results of mathematics could not in any way be attained without this
operation of abstraction. It is therefore necessary for logic to
distinguish sharply between good abstraction and bad abstraction.
It was not until I had been giving a large part of my time for
several years to tracing out the ways in which mathematical
demonstration makes use of abstraction that I came across a fact which
a mind which had not been scrutinizing the facts so closely |98| might have
seen long before, namely, that all collections are of the nature of
abstractions. When we pass from saying, "Almost any American can
speak English", to saying "The American nation is composed of
individuals of whom the greater part speak English", we perform a
special kind of abstraction. This can, I know, signify little to the
person who is not acquainted with the properties of abstraction. It
may, however, suggest to him that the popular contempt for
"abstractions" does not aim very accurately at its mark.
When I published a paper about number in 1882, I was already
largely anticipated by Cantor, although I did not know it. I however
anticipated Dedekind by about six years. Dedekind's work, although
its form is admirable, has not influenced me. But ideas which I have
derived from Cantor are so mixed up with ideas of my own that I could
not safely undertake to say exactly where the line should be |99| drawn
between what is Cantor's and what my own. From my point of view, it
is not of much consequence. Like Cantor and unlike Dedekind, I begin
with multitude, or as Cantor erroneously calls it, cardinal number.
But it would be equally correct, perhaps preferable, to begin with
ordinal number, as Dedekind does. But I pursue the method of
considering multitude to the very end, while Cantor switches off to
ordinal number. For that reason, it is difficult to make sure that my
higher multitudes are the same as his. But I have little doubt that
they are. I prove that there is an infinite series of infinite
multitudes, apparently the same as Cantor's alephs. I call the first
the denumerable multitude, the others the abnumerable multitudes, the
first and least of which is the multitude of all the irrational
numbers of analysis. There is nothing greater than these but true
continua, which are not multitudes. I cannot see that Cantor has ever
got the conception of a true continuum, such that in any |100| lapse of time
there is room for any multitude of instants however great.
I show that every multitude is distinguished from all greater
multitudes by there being a way of reasoning about collections of that
multitude which does not hold good for greater multitudes.
Consequently, there is an infinite series of forms of reasoning
concerning the calculus which deals only with a collection of numbers
of the first abnumerable multitude which are not applicable to true
continua. This, it would seem, was a sufficient explanation of the
circumstance that mathematicians have never discovered any method of
reasoning about topical geometry, which deals with true continua.
They have not really proved a single proposition in that branch of
mathematics.
Cayley, while I was still a boy, proved that metrical geometry,
the geometry of the elements, is nothing but a special |101| problem to
projective geometry, or perspective. It is easy to see that
projective geometry is nothing but a special problem of topical
geometry. On the other hand, since every relation can be reduced to a
relation of serial order, something similar to a scale of values may
be applied to every kind of mathematics. Probably, if the appropriate
scale were found, it would afford the best general method for the
treatment of any branch. We see, for example, the power of the
barycentric calculus in projective geometry. It is essentially the
method of modern analytic geometry. Yet it is evident that it is not
altogether an appropriate scale. I can already see some of the
characters of an appropriate scale of values for topical geometry.
My logical studies have already enabled me to prove some
propositions which had arrested mathematicians of power. Yet I
distinctly disclaim, for the present, all pretension to having been
remarkably successful in dealing with the heuretic |102| department of
mathematics. My attention has been concentrated upon the study of its
procedure in demonstration, not upon its procedure in discovering
demonstrations. This must come later; and it may very well be that I
am not so near to a thorough understanding of it as I may hope.
I am quite sure that the value of what I have ascertained will be
acknowledged by mathematicians. I shall make one more effort to
increase it, before writing this second memoir.
|
From Draft C - MS L75.129-132
|
I now pass to a rough statement of my results in regard to the
heuretic branch of mathematical thought. At the outset, I set up for
myself a sort of landmark by which to discern whether I was making any
real progress or not. Cayley had shown, while I was, as a boy, just
beginning to understand such things, that metric geometry, the
geometry of the Elements, is nothing but a special problem in
projective geometry, or perspective, and it is easy to see that
projective geometry is nothing but a special problem in topical
geometry. Now ma|130|thematicians are entirely destitute of any method of
reasoning about topical geometry. The 25th proposition of the 7th
book of the Éléments de Géométrie of Legendre, which is strictly all
that is known of the subject except some extensions of it, of which
the chief is Listing's census-theorem, was demonstrated with extreme
difficulty by Legendre, having exceeded the powers of Euler. Really
the proof is not satisfactory, nor is Listing's. The simple
proposition that four colors suffice to color a map on a spheroid has
resisted the efforts of the greatest mathematicians. If, then,
without particularly attending to that proposition or to topical
geometry, I find that my studies of the method of discovering heuretic
methods leads me naturally to the desired proof of the map-problem, I
shall know that I am making progress. From time to time, as I
advanced, I have tried my hand at that problem. I have not |131| proved it
yet, although the last time I tried I thought I had a proof, which
closer examination proved to contain a flaw. Since then, I have made,
as it seems to me, a considerable advance; but I have not been induced
to reexamine that subject, as I certainly should do if I were quite
confident of being able to solve it with ease. I have, however,
applied my logical theory directly with success to the demonstration
of several other propositions which had resisted powerful
mathematicians; and I have greatly improved upon Listing's theory; so
that I am confident that what I have found out is of value; and I
believe the same method has only to be pushed a little further to
solve the map-problem.
I can show that numbers, whether integral, fractional, or
irrational, have no other use or meaning than to say which of two
things comes earlier, which |133| later, in a serial arrangement. To ask,
How much does this weigh? is answered as soon as we know what things
among those which concern us it is heavier than [and] what it is
lighter than. A system of measurement has no other purpose than that;
and it appears to be the best artificial device for that purpose.
But all relations whatever can be reduced to relations of serial
order; so that every mathematical question can be looked upon as a
metrical question in a broad sense; and perhaps the best and readiest
way to get command of a branch of mathematics is to find what system
of measurement is best adapted to it. Thus, the barycentric calculus
applies to projective geometry [considered as] a sort of measurement;
and in fact modern analytic geometry results from just that
application. But it evidently labors under the difficulty of not
being a sufficiently flexible and well-adapted system of measurement.
Hermann Schubert's Cal|133|culus of Geometry gives some hint of what is
wanted.

End of PART 2 of 10 of MS L75

|